前回は、経営者の立場から、比較的、短い期間において、利益を最大化するにはどうするかを見てきました。しかし企業経営においては、「1年以内にこれだけ改善するには、どうするか?」といった短期の意思決定のほか、何年も先まで予測して打ち手を考える、長期の意思決定もあります。
長期の意思決定とは、今のインプットが何年にもわたってアウトプットを生むような企業活動に関するもので、たとえば、新しい機械を購入する、工場を新設/増設する、新たな製品の生産を始める、新しい事業を始めるといった活動が挙げられます。こうした長期的な企業活動の場合、今のインプットと、先々のアウトプットを比較しなければなりません。
さらに、投資したい案件がいくつもあると、最初の投資額(インプット)の大きさも、アウトプットの大きさやパターンも、案件により様々に異なることがあります。たとえば、最初の数年は急激にアウトプットが伸びてその後はアウトプットが出なくなるものもあれば、最初はアウトプットが小さいが一度軌道に乗ると大きなアウトプットが出るものもあります。こうした様々な案件を比較し、優先順位を付けることが必要です。
このように、時間的にズレのあるインプットとアウトプットをおカネの面で評価し、投資や資金調達における意思決定のベースになるフレームワークが、ファイナンスです。
金銭の時間的価値
では、時間的にズレのあるおカネを比較するには、どうすればよいでしょうか。ファイナンスでは、「今日の100円は明日の100円よりも価値がある」と考えます。なぜなら、今日100円を銀行に預ければ時間の経過とともに利子を生んでいくからです。
たとえば今日100円を年率5%の利子率で銀行に預金するとします(実際の銀行預金の金利より、かなり高いですが、あくまで分かりやすくするための例と考えてください)。5年後には
100×(1.05)5≒100×1.276=127.6円
となります。この127.6円のことを100円の5年後の「将来価値」と言います。一方、5年後に127.6円を受け取るためには、利子率が年率5%のもとでは今日
127.6円÷(1.05)5≒100円
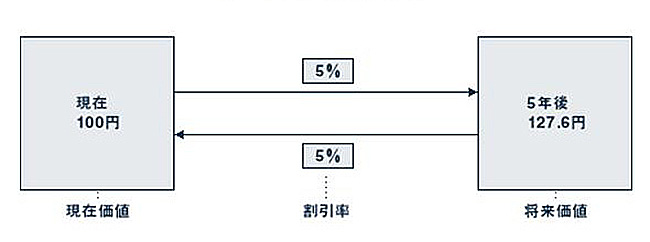
を銀行に預けなければいけません。この100円のことを5年後の127.6円の「現在価値」と言います。また、将来の価値から現在価値を求める際の利子率のことを「割引率」と呼びます(図表1を参照)。
割引率により、様々な時点のおカネを現在価値で比較することができます。たとえば同じ割引率5%を適用すると、8年後の140円の現在価値は約94.8円(=140円÷(1.05)8)ですから、5年後の127.6円よりも現在価値が低いことが分かります。
図表1 割引率と現在価値

また、ファイナンスでは、おカネを「キャッシュフロー」という捉え方で見ます。企業におけるキャッシュフローとは、ある期間に企業が稼いだ「儲け」として実際に手元に残った現金の総額を意味します。つまり、企業活動の結果、流入した現金(キャッシュ・イン)から、外部に流出した現金(キャッシュ・アウト)を差し引いた、残りの現金を指します。
A社の例で見てみましょう。社長の森田さんは、ある通信機器部品~製品Bとします~が今後も伸びると見て、その生産に使う機械を増設することを考えています。投資の初期には、機械の購入や設置などで多額のキャッシュ・アウトがなされます。一方で、その機械を使って製品Bを生産すると、製品Bの販売により毎年キャッシュ・イン(現金の受取り)が発生するとともに、原材料や人件費もかかるのでキャッシュ・アウト(現金の支払い)が発生します。毎年のキャッシュ・インとキャッシュ・アウトの差額が、A社がこの機械から得られる毎年のキャッシュフローとなります。
投資の価値を計る
ファイナンスでは、A社の機械のような資産の金銭的価値は、それらが将来生み出すキャッシュフローの現在価値で計ります。そして、資産の金銭的価値を、それらが将来生み出すキャッシュフローの現在価値として求める方法を、「DCF(Discounted Cash Flow)法」と呼びます。
企業がある資産への投資を行うか否かを決定するときには、その投資から得られるキャッシュフローの現在価値から初期投資額を差し引いた差額を見ます。この差額を、投資の「NPV(Net Present Value、正味現在価値)」と呼びます。NPVがプラスであれば、投資によって企業にプラスの経済的な価値がもたらされることを意味します。従って、NPVがプラスならば「投資を実行すべき」であり、マイナスならば「投資はやめるべき」となります。また、いくつかの投資案件を比較する場合は、NPVが大きいほど経済的な価値が大きいことになります。
先ほどのA社の例で、製品Bを生産する機械Xへの投資を考えてみましょう。条件は以下の通りです(キャッシュフローのイメージは図表2を参照)。
割引率を5%とする
初年度は、機械Xの購入と設置等で、1000万円かかる
毎年のキャッシュフロー(=毎年の「キャッシュ・イン-キャッシュ・アウト」)は:
1年目300万円、2年目350万円、3年目~5年目400万円
5年後には製品Bの生産をやめる。このときの機械Xの撤去費用は、
機械Xの売却代金と差し引きして0になる
1年目以降5年目までの各年のキャッシュフローの現在価値は:
1年目:300万円÷1.05=285.7万円
2年目:350万円÷(1.05)2=317.5万円
3年目:400万円÷(1.05)3=345.5万円
4年目:400万円÷(1.05)4=329.1万円
5年目:400万円÷(1.05)5=313.4万円
従って、キャッシュフローの現在価値は
285.7万円+317.5万円+345.5万円+329.1万円+313.4万円=1591.2万円
となり、今手元に1591.2万円を持っている場合と等しい経済的な価値をもっているといえます。ここから、初期投資の1000万円を差し引いて、NPVは591.2万円(=1591.2万円-1000万円)となります。
次に、製品Bを生産する機械として、機械Yも候補にあがっています。この機械Yは機械Xよりも初期投資がかさみます。機械XはA社が今まで使用してきた機械と同じですが、機械Yは新型で操作法が違い、扱い方に慣れる必要があるなどの理由で、1年目のキャッシュフローは少なめです。ただし、その後は機械Xよりも性能が良いため、キャッシュフローを多く生み出します。機械Yの条件は以下の通りです。
初年度は、機械Yの購入と設置などで、1500万円かかる
毎年のキャッシュフロー(=毎年の「キャッシュ・イン-キャッシュ・アウト」)は:
1年目250万円、2年目450万円、3年目500万円、4年目550万円、5年目600万円
割引率と、5年後の扱いについては、機械Xの場合と同様とします(キャッシュフローのイメージは図表2を参照)。機械Xの場合と同様に計算すると、機械Yから得られるキャッシュフローの現在価値は2000.8万円、初期投資の1500万円を差し引くとNPVは500.8万円となります。
機械X、機械YともNPVがプラスなので、実行する価値はあると言えます。ただし、機械Xと機械Yのいずれかを選択する場合は、NPVの大きい機械Xの方が経済的価値は高いので、こちらを選ぶべきということになります。
図表2 A社投資案件のキャッシュフロー

ここまで機械を購入する例で見てきましたが、工場の新設でも、新製品、新規事業でも、考え方は同じです。さらに、企業はいわば様々な投資案件の集合体と見ることができるので、企業の価値も、企業が将来、生み出すキャッシュフローの現在価値と捉えることができます。違いは、キャッシュ・インやキャッシュ・アウトの見積り方、割引率の求め方が、もっと複雑になることです。こうした複雑なケースを学ぶ際にも、図表2のようなキャッシュフローの図を描き、イメージで大枠を捉える癖をつけると、理解しやすくなるでしょう。
(本稿は、グロービス・オーガニゼーション・ラーニングが発行するメールマガジン「グロービスNews」の2003年4月25日号に掲載されたものを、加筆修正のうえ再掲したものです)。

































.jpg?fm=webp&fit=clip&w=720)





.jpg?fm=webp&fit=clip&w=720)
