今年7月発売の『ビジネスで使える数学の基本が1冊でざっくりわかる本』から「Chaper6標準偏差」の一部を紹介します。
世の中の多くの統計数字には正規分布を描くものが少なくありません。身長などはその典型ですし、工業製品製造におけるスペックの数字からのズレなどもその典型です。正規分布の便利なのは、平均から±1σの範囲に68%、±2σの範囲に95%入るなど、存在確率が明確なことです。それゆえ工場におけるTQC(Total Quality Control:統合的品質管理)などでも多用されるわけです。一方で気をつけるべき点も多々あります。その1つに、正規分布表の端の方に行くと(すなわちσが大きくなると)、異なる2つの集団の差が過剰に大きく見えてしまうという点があります。世の中、目立つのはこうした特別なサンプルであることは多いものです。ずば抜けた実績を残した人物などはその典型です。人は往々にしてそのバックグラウンドを見て「Aという特性のバックグラウンドの人はBという特性のバックグラウンドの人に比べて業績を残しやすいんだ」と考えることがありますが、それは必ずしも適切ではないことが多いのです。こうした正規分布の落とし穴を知っておくことも、世の中を正しく理解する上で非常に重要です。
(このシリーズは、グロービス経営大学院で教科書や副読本として使われている書籍から、東洋経済新報社のご厚意により、厳選した項目を抜粋・転載するワンポイント学びコーナーです)
◇ ◇ ◇
正規分布
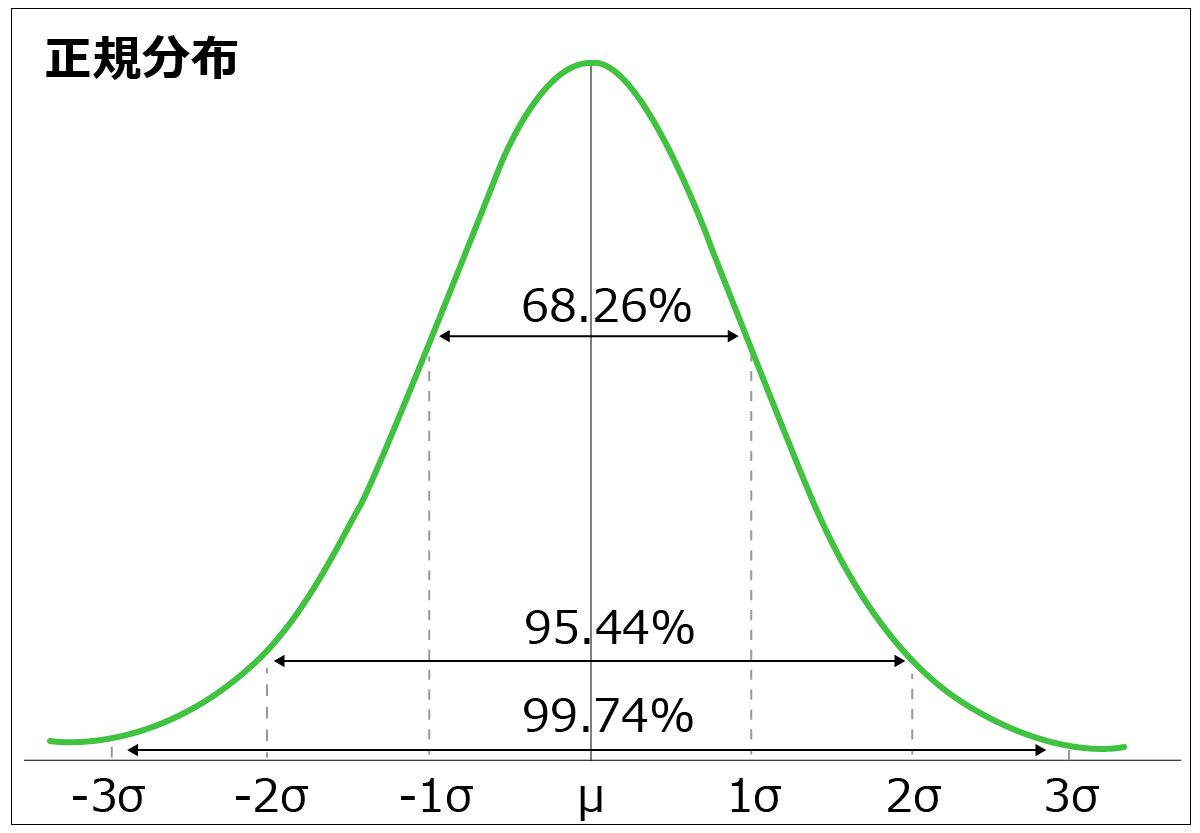
筆者はアメリカのプロフットボールが好きなのですが、その試合を観ていると、最も俊敏さや足の速さを求められるコーナーバックというポジションはほとんどがアフリカ系アメリカ人です。
多くの人は、「アングロサクソン系に比べると、圧倒的にアフリカ系アメリカ人の方が足が速い」と思うかもしれません。しかし、本当にそう言い切れるでしょうか。単純化して考えてみましょう。
G国は2つの人種(A人とB人)からなる国とします。A人とB人の20代男性はそれぞれ100万人とします。
A人の20代男性の平均100m走記録は14秒、標準偏差は1.0秒、B人の平均100m走記録は14.5秒、標準偏差は1.0秒とします。標準正規分布表を用いて、それぞれの人数を求めてみましょう。
- 14秒以内で走る20代男性
A人:100万人×0.5=50万人
B人:100万人×(0.5-0.191)=30.9万人 - 13秒以内で走る20代男性
A人:100万人×(0.5-0.341)=15.9万人
B人:100万人×(0.5-0.433)= 6.7万人 - 12秒以内で走る20代男性
A人:100万人×(0.5-0.477)=2.3万人
B人:100万人×(0.5-0.494)=0.6万人 - 11秒以内で走る20代男性
A人:100万人×(0.5-0.4987)=1300人
B人:100万人×(0.5-0.4998)=200人 - 10秒以内で走る20代男性
A人:100万人×(0.5-49997)人=30人
B人:100万人×(0.5-0.499997)人=3人
ここでのポイントは、足が速くなるにしたがって(つまり、正規分布の端に行くにしたがって)、A人の占める比率が高まることです。
プロフットボールの選手はまさにこの端の部分に相当します。実は正規分布の端に行くほど、それぞれの集団の特徴が強調される傾向があるのです。
極端な特徴が表れる端の部分を全体の代表と思い込んでしまうのは、それゆえに誤りです。
バスケットボールなどもアフリカ系アメリカ人が多いスポーツですが、だからといってアフリカ系アメリカ人が皆、バスケットボールが非常にうまいわけではないのも同様です。
『ビジネスで使える数学の基本が1冊でざっくりわかる本』
著者:グロービス 執筆:嶋田毅 発行日:2022/7/29 価格:1,760円 発行元:東洋経済新報社


































.png?fm=webp&fit=clip&w=720)
.jpg?fm=webp&fit=clip&w=720)

