問題です
以下のAさんの問題は何か。
A: 「僕は、出身大学の偏差値というか、学校の勉強ができるかできないかということと、仕事ができるできないは無関係だと思うね。さらに言えば、学歴と仕事の能力も無関係だと思う」
B: 「それはさすがにありえないだろう。じゃあなぜみんな苦労してまで、より良い大学に行こうとするんだい?」
A: 「それは皆が勘違いしているんだよ。良い学校に行けば仕事もできるとみなされて給料の良い仕事にありつけるだろうってね」
B: 「でも、実際に偏差値が高い学校の人間の方が仕事はできるんじゃないのか。事実、大企業の社長や官僚なんかは世間で言う良い大学の出身者が多い」
A: 「それは一面的なものの見方だよ。実際、大学を出ていなくても世の中には仕事ができる人はいくらでもいる。ウチのC課長だって高卒だけど、間違いなく取締役になるはずさ。ひょっとしたら社長になるかもしれない」
B: 「たしかにC課長は優秀だけど、彼は例外という気もするしなあ」
A: 「逆に、Dさんは超有名大学を出ているけど、絶対に出世しそうにないじゃないか」
B: 「まあ、そうだけど」
A: 「有名どころだと、スティーブ・ジョブズだって、決して有名な大学に行っていたわけではないし、しかも結局中退したから、学歴でいえば高卒ということになる。しかし、アップルを時価総額1位の企業に復活させた。ときどき『こんな時代に彼のような政治家がいれば』と待望論がでる田中角栄だって、高校すら出ていないけど、東大出身の官僚たちを自在に使いこなした」
B: 「うーん」
A: 「いずれにせよ、学校のお勉強と仕事の能力には本質的には関係なんてないんだよ」

解答です
今回の落とし穴は、「無相関と弱い相関の混同」です。正式な名称はないようなので、ここではこう呼ぶことにします。これは、本来はある程度の相関関係があるにもかかわらず、例外が多いことを理由に「相関(関連性)なんてない」と考えてしまうことです。
念のためにおさらいしておくと、相関とは、2つの変数の間に何らかの法則性、連動性がある状態を言います。たとえば、気温が高くなればビールの売上げも上がる、気温が低ければビールの売上げも下がるという連動性がある場合、気温とビールの売上げには相関があると言います。
相関には「強さ」があり、それを数値で表したものが相関係数です。相関係数は、「一方が大きくなれば他方が大きくなる」という関係が強いほど1に近づきます。相関係数の絶対値がゼロに近づくほど相関が弱いことを意味します。相関係数がゼロの場合、2つの変数は全く無関係(独立している)ということになります。
実際の社会においては、相関係数が1になる完全な相関はほとんどありません。相関が1になる関係とは、散布図を描いて回帰直線を引いた時に、すべてのサンプルがその直線上に乗るという関係です。
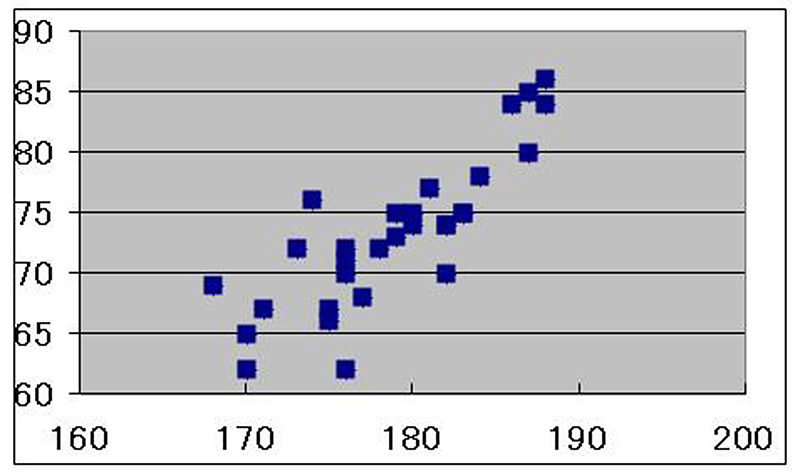
現実を見ると、たとえばプロサッカー選手の「身長」と「体重」といった、比較的相関の強い変数間でも、相関係数は0.8程度です(図1参照)。逆に言えば、回帰直線から多少外れる選手は必ずいるということです。
図1:あるプロサッカーチームの選手身長(cm)と体重(kg) 相関係数は0.84

図1の例は、相関係数が0.84と高めであるため、「身長の高い選手ほど体重もある」という関係がまだ概ね成り立っています。
図2:あるプロ野球チームの投手身長(cm)と体重(kg) 相関係数は0.55

ところが、図2のように相関係数がやや低くなると、全体的な傾向としては確かに「身長の高い選手ほど体重もある」とは言えるものの、個別にみると、「身長が高いのに体重があまりない選手」や「身長は低いのに体重が非常にある選手」などが目立ってきます。
局所的に見ると、「A選手はB選手に比べ、身長は10cm低いのに15kg以上体重がある」といった、全体の傾向とは大きく逆転した組み合わせも出てきます。しかし、こうした大きく逆転した組み合わせがあるからといって、「身長と体重には関係がない」と言ってしまうのは、図からも明らかに不適切です。
おそらく、冒頭のケースで出てきた、「学校の勉強ができるかできないか」と「仕事ができるかできないか」も、この弱い相関の例と思われます。個別に見れば全体の傾向から大きく逸脱した人も確かにいるでしょう。しかし、だからといって、「学校の勉強ができるかできないか」と「仕事ができるかできないか」に全く関係がないかと言えば、そんなことはないでしょう。
「『仕事ができるかできないか』は『学校の勉強ができるかできないか』だけで決まるわけではない」あるいは「『学校の勉強ができるかできないか』は、ある程度『仕事ができるかできないか』に関係してくるがが、その程度は決して強くない」という主張の方が納得感は高かったはずです。
今回のAさんのような、無相関と弱い相関を混同した主張はよくなされますが、多くは、先述の例のように「○○が高いにもかかわらず、△△が低い人間はいる」といった、全体の傾向から外れたサンプルの存在をその根拠にしています。これらは、相関があったとしても弱い相関であれば必然的に発生するものであり、それを根拠に無相関を主張するのは行きすぎです。
それにもかかわらず、そうした主張がなされる理由としては、人間は目立つ特異点に意識が引っ張られすぎる傾向があるということや、そもそも「そんな傾向なんてない」と思い込みたいがゆえに、正式なリサーチなどの裏付けもなく、特異点(全体の傾向から大きく乖離した点)のサンプルを必要以上に強調してしまう、といったことが考えられます。
後者の理由について言えば、デリケートな問題ほど、そうした傾向が強くなるきらいがあるようです。「身長が高い人ほど指が太い」という話であれば気色ばんでそれに反論する人もいないでしょう。しかし、「身長が高い人ほど収入が高い傾向にある」と言うと、「収入」というデリケートな問題だけに、たくさんの反論、反例が出てくるのです。冒頭のケースも同様です。
相関関係の有無や強弱の把握は、ビジネスのヒントを得る上でも非常に有効です。ビジネスパーソンとしては、思い込みに捉われたり一部の特異点に過度に引っ張られたりするのではなく、全体感を持って、冷静に現実の姿を見極めたいものです。
*本連載は、次回2012年2月16日が最終回となります。