問題です
以下の考え方の問題点は何でしょうか
「アメリカのNBA(プロバスケットボールリーグ)なんかを見ていると、各チームの主力や、オールスターに選ばれる選手は、ほとんどがアフリカ系アメリカン人だ。短距離走の選手なんかもそうだ。やはり、白人に比べると、アフリカ系アメリカ人の方が、はるかにバスケットボールや短距離走のセンスがあるんだろうな」

解答です
今回の落とし穴は、異常値一般化の罠です(正式な用語ではないのですが、ここではこのように呼びます)。これは、分布図の端(全体からみれば異常値の領域)に行くにしたがって顕著になる集団間の差異を見て、その差異を全体的な傾向と勘違いしてしまうというものです。なお、集団の分布にはさまざまなものがありますが、今回は、最も自然に見られる分布である「正規分布」を前提に議論を進めます。
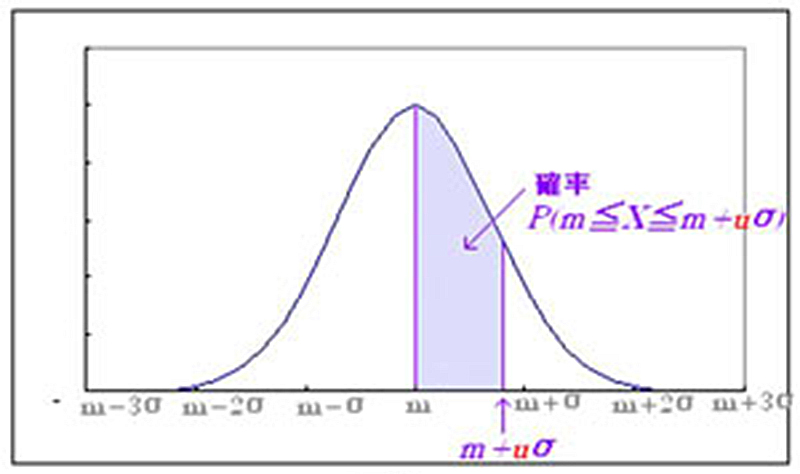
まず、正規分布とは何だったか、おさらいしてみましょう。正規分布とは、ある標本集団のばらつきが、その平均値を中心に左右同型の釣鐘状になるような分布です(図表1)。たとえば、ある民族の身長や、工業製品の規格からの誤差などは、ほぼ、正規分布に近い形になります。道行く人にいきなりダーツをやらせてみて的の中心からの距離を測ってみたら、これも正規分布に近い分布になるでしょう。

正規分布が様々な研究や生産工学などの統計処理に用いられる理由として、その数学的な扱いやすさ、特に、確率分布に関する扱いやすさがあります。まず、それを確認しましょう。
図表1において、mは平均、σは標準偏差を表します。正規分布では、mからm+uσに含まれる確率が簡単に計算できるというメリットがあります。たとえば、u=1、すなわち、mからm+σには、全体のおよそ34%が含まれることが知られています。言い方を変えると、平均から、±1σ(標準偏差)の間には、およそ68%の標本が含まれるということです。ちなみに、これが±2σだとおよそ95%、±3σでは、およそ99.7%が含まれることになります(参考までに、標準正規分布表を載せたサイトを1つ紹介しておきます。http://staff.aist.go.jp/t.ihara/normsdist.html)。
さて、ここで2つの正規分布、A民族とB民族の男性の身長を考えてみましょう。A民族の男性は平均身長170cmで標準偏差6cm、B民族は平均身長173cmで標準偏差は同じく6cmとします。画にすると図表2のようになります。

ここで、この2つの民族の男性について、ある身長の範囲に収まる人口の率を求めてみましょう。範囲を3cm(すなわちこのケースでは0.5σ)ずつずらしていきます。

この表から分かる通り、平均値付近ではそれほど大きくなかった両民族の差異(A民族/B民族比)が、分布の端に行くにしたがって、どんどん広がっていくことが分かります。つまり、全体的に見れば両集団に大きな差がない場合でも、標準偏差が±3を超えるような「異常値」付近では、両集団の差異が強調されて現われてしまうのです。
プロバスケットボール選手になるような人々は、おそらく全体から見たら3σどころか5σレベルの人々でしょう(実際に、アメリカ人男性全体で、およそ50万人に1人)。そうした「異常値の世界」における母集団同士の比は、全体の傾向から大きく逸脱してしまうのです。したがって、プロ選手の中のさらにエリート集団だけを見て、集団間の差異として一般化してしまうのは大きな過ちなのです。
前々回の「生存バイアスの罠」にも通ずる話ですが、我われが見る世界は、往々にして全体ではなく、「一部の選ばれし者」の世界であることが少なくありません。「大企業の社長」、「国会議員」、「有名タレント」なども、おそらく「異常値の世界」の人々です。
我われはしばしば、ある人々を見たときに、その属性(年齢、性別、出身地、出身校等)を気にします。しかし、上記のような非常に目立つ人々の属性は、必ずしもマスの傾向を正確には反映しないのです。そうしたセンスを持ちながら世の中を冷静に眺める癖をつけたいものです。