前回は、仮説を検証するための情報の集め方について解説した。今回からは実際にデータ(数字)を分析する際の留意点などについて話を進めていく。
数字を分析するには大きく2つの方法がある。1つは数多くのデータを一つの数字に集約し全体像を浮き彫りにする方法。平均、中央値、最頻値などの概念が含まれる。もう1つは様々な角度からデータを切り取り、特徴をつかんでいく方法だ。時系列分析、ヒストグラム分析、相関分析などの概念が含まれる。
全体を1つの数字に集約する方法をみていこう。最もよく使われる分析方法の1つであり、平均値や分散(データのばらつき度)を活用する。中学、高校の時から、データが並んでいたらまず平均値や分散を計算してみるというのが習慣になっている人も多いだろう。このようなデータの集合を1つの数字で代替して表現する数字を「代表値」という。
代表値は実は色々な意味で悩ましい。例えば単純にデータを合計してデータ数で割る単純平均の場合、個別のデータの重要性は全て等しい、との前提に基づいていることをしっかり理解しているだろうか。
喫茶店経営をイメージしてみてほしい。単価500円のオレンジジュース、単価300円のコーヒー、単価600円のココアを販売している場合、商品の単純平均単価は、(500+300+600)÷3=約467円となる。
一方、それぞれ1日に10杯、20杯、5杯売れたとすると、客単価(販売数を加味した加重平均)は400円となり、全く違う意味の数字となる。
このような極めて単純な話でも、何のための分析なのかという分析の目的、つまりイシューをしっかりおさえておくことが何よりも重要なのだ。さもないと、単なる数字遊びになってしまう。
平均でみるというのは、個別データの個性を「全て無視」しようとする作業である。そのため、今からやろうとしている分析は、代表値に語らせるべき話なのかどうかをそもそも吟味しなければならない。特にデータ数がそれほど多くない場合などには、留意が必要だ。
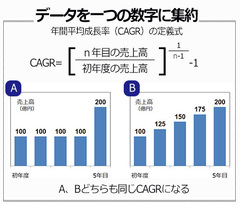
次に、年間平均成長率(CAGR)をみてみよう。これは、□年度から△年度までの○年間で、平均的に何%成長しているかをあらわす。定義式は図のようになる。新聞、雑誌などで年間平均成長率と記載がある場合は、この数字で計算された数字のはずだ。最後の年度の数字÷最初の年度の数字の結果を年数で割るようなことをしてはいけない。
定義式を見れば一目瞭然だが、この数字を算出するには、最初の年度の数字と最後の年度の数字の2つしか使わないことがわかる。つまり、Aのような成長軌道でも、Bのような成長軌道でも同じCAGRの数字になるということだ。
一瞬、「えっ?」という印象を持たれる人も多いのではないかと思う。この「えっ」を少なくするための方法は、ただ一つ。いきなり表計算ソフトの関数で数字だけを計算するのではなく、その前に、目に見える何らかの方法でグラフにしてみるといった「一手間をかける」ということだ。数字そのものを見る、それを絵にしてみる、このコンビネーションをぜひ駆使してほしい。
平均値などは誰でもがピンとくる概念だけに、一旦数字として出してしまうと独り歩きを始める可能性も高い。十分に配慮したいものだ。

※この記事は日本経済新聞2013年9月4日に掲載されたものです。
(Coverphoto:shutterstock/Ismagilov)
◆次の回はこちら
◆連載一覧はこちら